1) O que é a
Força elástica?
É uma força restauradora, aplicada a corpos
com elasticidade, em particular, as molas.
2) Como se
aplica a força elástica?
O sentido da força elástica é sempre o de
restaurar à posição de equilíbrio.
3) Como
calcula-se a força elástica?
Fórmula determinada pela lei de Hooke: Fel =
k ⋅ x
k é a constante elástica do corpo elástico
(ou da mola) e é dependente da natureza do material que é feito.
x é a deformação sofrida pela mola (seja de
distensão ou compressão).
4) Calcule a força elástica necessária para comprimir uma mola em 20 cm
(constante elástica da mola = 150 N/m).
Colhendo os dados do problema temos:
x = 20 cm = 0,2 m
k = 150 N/m
5) Resolução
Usando a fórmula da força elástica:
Fel = k ⋅ x
Fel = 150 x 0,2
Fel = 30 N
6) Como se caracteriza a Força de Tração?
É uma Força que tem a função de transmitir outras forças.
7) Como se aplica a Força de Tração?
Está
associada a cordas, cabos e fios em geral.
8) Como se calcula a Força de Tração?
Não
existe fórmula para calcular a tração. Temos que fazer a análise das forças que
atuam no problema, considerando-se a 2a lei de Newton.
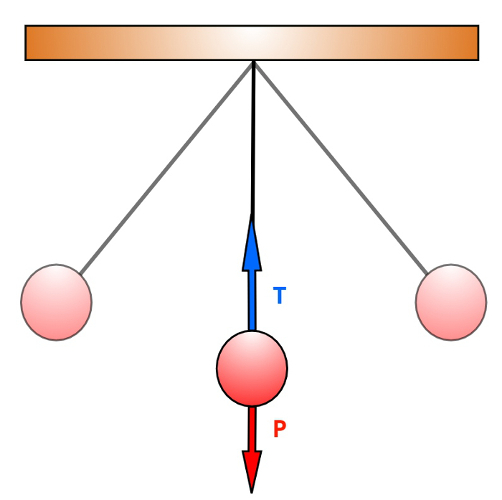
9) Exemplo de Aplicação da Força de Tração:
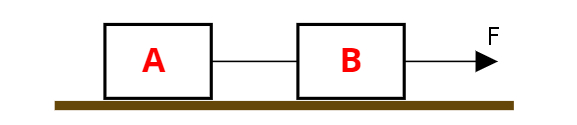
Na figura, temos dois blocos ligados por um fio ideal; o bloco
"A" pode deslizar sem atrito pela superfície horizontal.
Sabendo que mA = 8 kg e mB = 12 kg e g
= 10 m/s2, calcule a força de tração no fio.
Usando a 2ª lei de Newton no bloco B temos:
FR = PB −
T
PB − T
= mB ⋅ a (1)
Usando a 2ª lei de Newton no bloco A:
FR = T
T = mA ⋅
a (2)
Associando as equações (1) e (2), temos:
PB − mA ⋅ a = mB ⋅ a
10) Resolução:
Substituindo os valores, encontramos a
aceleração do sistema:
120 − 8∙a = 12∙a
120 = 12∙a + 8∙a
120 = 20∙a
a = 120/20
a = 6 m/s2
Substituindo o valor de aceleração (a) na
equação (2), encontra-se a tração (T):
T = mA ⋅
a
T = 8 x 6
T = 48 N
10) Que condições são necessárias para que um corpo esteja em equilíbrio
entre as forças?
Um corpo está em equilíbrio quando a somatória de todas as
forças que atuam sobre ele for nula, ou seja, igual a zero. De acordo com a
Primeira Lei de Newton, quando a resultante das forças que atuam sobre um corpo
é nula, o corpo permanece em seu estado de repouso ou em movimento retilíneo
uniforme.
Disso, surgem as ideias de equilíbrio estático e dinâmico.
O equilíbrio estático
acontece quando a força resultante sobre o corpo é nula e este objeto
se encontra em repouso, ou seja, não possui velocidade.
Quando um objeto se encontra em movimento retilíneo uniforme, não
há aceleração, e por esse motivo, também não existe força resultante. Como
a força é nula e o objeto possui velocidade constante, dizemos que o corpo se
encontra em equilíbrio dinâmico.
Atividades:
1) Como se chama a força que tem a função restauradora, aplicada a corpos com elasticidade, em particular, as molas?
(A) Tração
(B) Elástica
(C) Normal
(D) Peso
2) Como se chama a força que
tem a função de transmitir outras forças e está associada a cordas, cabos e
fios?
(A) Tração
(B) Elástica
(C) Normal
(D) Peso
3) De acordo com a Dinâmica,
dizemos que um corpo está em equilíbrio quando:
(A) seu movimento é retilíneo.
(B) sua aceleração é constante.
(C) sua aceleração é nula.
(D)
o módulo da força resultante sobre o corpo é maior que zero.
4) Em relação à força
elástica, descrita matematicamente pela lei de Hooke, assinale a
alternativa CORRETA:
(A) Quanto maior for a constante elástica
de uma mola, menor será a força necessária para deformá-la.
(B)
A força elástica é inversamente proporcional à elongação da mola.
(C)
A força que é exercida sobre a mola, deformando-a, é igual à força elástica
gerada pela mola.
(D) A força elástica tem o seu valor
máximo quando a mola encontra-se em seu formato original.
5) Calcule a força elástica
necessária para comprimir uma mola em 60 cm (constante elástica da mola =
160 N/m):
(A) 60 N (B) 96 N (C) 160 N (D) 200 N
6) A qual lei de Newton está associada a força de Tração?
(A) Inércia
(B) Dinâmica
(C) Ação e Reação
(D) Gravitação Universal
7) Veja a figura abaixo, nela temos um bloco de massa m = 8
kg suspenso por uma corda. Adotando g = 10 m/s2, determine o valor
da tração na corda.
(A) É igual à força Peso em módulo, 80
N, em sentido contrário.
(B) É igual à força Normal em módulo, 8
N, no mesmo sentido.
(C) Tem módulo igual à força de
resistência do ar, 10 N, em sentido contrário.
(D) Tem o mesmo sentido da força Peso,
com módulo de 160 N.
8) Suponha que uma pessoa de massa igual a 50 kg esteja suspensa numa corda, como na ilustração abaixo. A outra extremidade dessa corda está presa num bloco de massa de 56 kg que está em repouso em uma superfície plana. Supondo que a aceleração da gravidade local é igual a 10 m/s2, identifique as forças presentes no sistema e determine o valor da força de reação normal trocada entre o bloco e a superfície onde está apoiado.
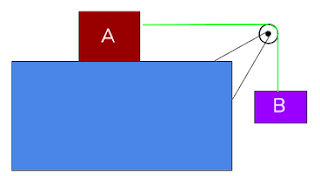
9) Dois blocos, A e B,
de massas iguais a 8 kg e 2 kg, respectivamente, estão representados na figura
abaixo. Os blocos são unidos por um fio inextensível e puxados por uma força F
de módulo igual a 20 N. Determine:
a) Aceleração do sistema
b) Tração no fio
10) Dois blocos, A e B,
de massas iguais a 7 kg e 3 kg são ligados por um fio inextensível como mostra
a figura abaixo. Calcule a aceleração do sistema e a tração nos dois fios.
11) A respeito de uma
partícula em equilíbrio, é a afirmativa FALSA:
(A) Não recebe a ação de forças.
(B) Pode descrever trajetória retilínea.
(C) Pode estar em repouso.
(D) Pode ter altas velocidades, desde que seja
constante.
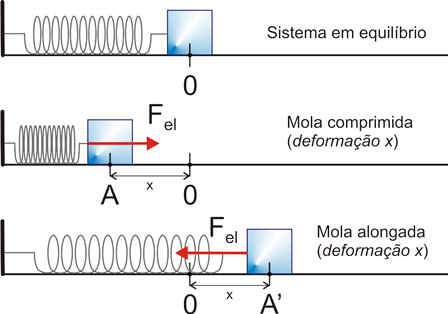
12) No esquema abaixo, temos um corpo de massa m preso a uma corda que passa por uma roldana e que está ligada a
uma mola de constante elástica k. A
mola sofre uma deformação x em
virtude da atuação do peso do bloco. A respeito das forças peso e elástica,
marque a alternativa correta:
(A) A força elástica não pode ser considerada a reação da força peso, pois, nesse caso, essas duas forças atuam sobre o bloco de massa m.
(B) A força elástica é inversamente
proporcional à deformação causada pela força peso.
(C) A força de tração
existente na corda é quem puxa e deforma a mola.
(D)
Quanto maior for a constante elástica k
da mola, mais fácil será a sua deformação.
Enem - 2016
Uma invenção que significou um
grande avanço tecnológico na Antiguidade, a polia composta ou a associação de
polias, é atribuída a Arquimedes (287 a.C. a 212 a.C.). O aparato consiste em
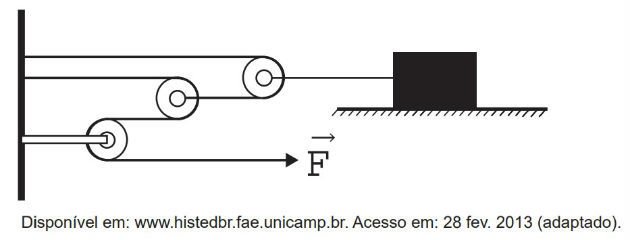
associar uma série de polias móveis a uma polia fixa. A figura exemplifica um
arranjo possível para esse aparato. É relatado que Arquimedes teria demonstrado
para o rei Hierão um outro arranjo desse aparato, movendo sozinho, sobre a
areia da praia, um navio repleto de passageiros e cargas, algo que seria
impossível sem a participação de muitos homens. Suponha que a massa do navio
era de 3 000 kg, que o coeficiente de atrito estático entre o navio e a areia
era de 0,8 e que Arquimedes tenha puxado o navio com uma força ,
paralela à direção do movimento e de módulo igual a 400 N. Considere os fios e
as polias ideais, a aceleração da gravidade igual a 10 m/s2 e
que a superfície da praia é perfeitamente horizontal.
(A) 3. (B) 6. (C) 7. (D) 8. (E) 10.
As forças
que atuam no barco estão representadas no diagrama abaixo:
Pelo diagrama,
notamos que o barco, para sair do repouso, é necessário que a força de tração T
seja maior que a força de atrito estático máxima. Para calcular o valor desta
força, iremos usar a fórmula:
Sendo nesta situação o módulo do peso igual ao módulo da força normal, temos:
Substituindo os valores informados, temos:
Fatritomáx =
0,8 . 3000 . 10 = 24 000 N
Sabemos que a força
F exercida por Arquimedes foi igual a 400 N, então, esta força deverá ser
multiplicada por um certo fator para que o seu resultado seja maior que 2400 N.
Cada polia móvel
utilizada dobra o valor da força, ou seja, fazendo uma força igual a F, a força
de tração (força que irá puxar o barco) será igual a 2F.
Usando os dados do
problema, temos a seguinte situação:
1 polia → 400 . 2 =
400 . 21 = 800 N
2 polias → 400 . 2 .
2 = 400 . 2 2 = 1600 N
3 polias → 400 . 2 .
2 . 2 = 400 . 23 = 3200 N
n polias → 400 . 2n >
24 000 N (para sair do repouso)
Desta forma,
precisamos conhecer o valor do n, então:
Sabemos que 25 = 32 e que 26 = 64, como queremos encontrar o número mínimo de roldanas móveis, então ao utilizar 6 roldanas já será possível movimentar o barco.
Alternativa: (B) 6














Nenhum comentário:
Postar um comentário