Hidrostática

1) Já estudamos diversas maneiras de descrever o movimento em objetos, corpos e partículas no estado sólido da matéria. Porém é possível a Física pode estudar o movimento nos gases como o ar e nos líquidos como a água?

Já aprendemos que os objetos se atraem e os que estão próximos à Terra, são atraídos para sua superfície. Envolvendo a Terra, existe uma camada formada por gases. Essa camada recebe o nome de atmosfera. A atmosfera contém, entre gases, oxigênio, que é essencial á vida. Os gases são formados por conjuntos de átomos, chamados moléculas. Essas moléculas possuem massa e são atraídos para a Terra, mantendo-se, assim, ao seu redor. Existem muitas dessas moléculas envolvendo a Terra e sendo atraídas em sua direção. Cada uma delas é extremamente leve, pois sua massa é muito pequena, mas, como existem muitas delas, o peso de todas juntas é considerável. Esse movimento dos gases na atmosfera é descrito e estudado como a Física dos Fluidos.

Bem como, a interação da atração da Terra às substâncias que estão na forma líquida da matéria presentes no globo terrestre, como a água, essencial também à vida humana.

2) O que são fluidos?

Todos os materiais não sólidos apresentam uma característica interessante: podem escoar; por isso são chamados de fluidos, é o que vemos em como nos óleos lubrificantes, no ar, no sangue, na água, no gel e loções de barbear.

Além da capacidade de escoar, os fluidos líquidos assumem a forma do recipiente que os contém, mesmo que seja necessário um grande intervalo de tempo para que isso ocorra, como no caso do piche, ou em intervalo ainda maior, como no caso do vidro, que também é considerado fluido.

Outra característica dos fluidos é a capacidade de, ao receber uma força, transmiti-la igualmente a todos os pontos. Isso garante uma uniformidade quando, por exemplo, um balão ou câmara de ar é preenchido com ar.

3) Como é chamada e medida essa capacidade dos fluidos de ocupar lugar no espaço ou no recipiente que a contém e como isso é dado?

Volume é a capacidade de todos os corpos ocuparem lugar no espaço. No caso, dos fluidos, eles ocuparão o espaço no qual ele estiver contido que vai depender do formato do recipiente e das suas dimensões como a área da base do recipiente e sua altura. Em particular, os gases possuem volume variável e preenchem totalmente o volume do recipiente que o contem, ao passo que os líquidos têm volume quase invariável, ou seja, são praticamente incompreensíveis.

4) Como é estudado a relação dos fluidos com as forças que interagem com eles?

A interação das forças nos fluidos permite que os pneus dos carros e bicicletas, por exemplo, quando cheios de ar, tenham uma aparência uniforme em toda sua extensão. Essa particularidade nos permite aplicar o conceito de pressão para os fluidos, uma vez que ele relaciona o valor da força aplicada com a superfície de contato.

5) Qual que diz o conceito de pressão?

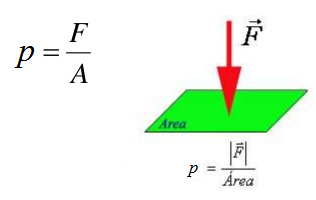
Define-se pressão (p) como sendo a relação entre a força (F) exercida perpendicularmente sobre a superfície e a área (A) dessa superfície.

p = F / A

No SI, a unidade padrão de pressão é o pascal (Pa).

1 Pa = 1 N/m².

Porém outras unidades são também utilizadas: atm, mmHg, kgf/cm², lbf/pol².

Essa relação explica, por exemplo, porque facas afiadas cortam melhor que as que não afiadas: as afiadas exercem muita pressão sobre o que quer cortar. Quanto mais afiada, menor é a área de contato e, consequentemente, maior a pressão exercida.

Concluindo: a pressão de uma força aplicada a uma superfície é igual à intensidade da força aplicada, dividida pela área da superfície onde essa força é aplicada.

6) O que vem a ser a pressão atmosférica?

Como vimos no início desta aula, ao nosso redor e acima de nossas cabeças existe ar, e esse ar tem peso; logo, ele irá exercer pressão sobre nosso corpo. E não apenas sobre ele, mas também sobre toda a superfície da Terra. Essa pressão é chamada pressão atmosférica. Pressão atmosférica é a pressão que a atmosfera exerce sobre a superfície da Terra.

Agora veja: se a pressão depende diretamente da força, nesse caso, o peso do ar, e este depende da quantidade de moléculas que existe, então quanto menor for a espessura da atmosfera e a concentração das moléculas, menor será a sua pressão e vice-versa. Portanto, a pressão atmosférica diminui com a altitude, isto é, com a altura do local, em relação ao nível do mar.

7) Como é a pressão é exercida nos fluidos líquidos?

Todo líquido exerce pressão nas paredes do recipiente que o contem e uma das características do líquido é transmitir pressão.

Quando mergulhamos em uma piscina, lago, rio ou mar, nosso organismo passa a suportar, além da pressão do ar, a da água. Não estamos adaptados para viver em meio líquido, pois, além de precisarmos respirar, a resistência à pressão nas variadas partes do corpo é muito diferente, como é o caso do tímpano e dos olhos. E quanto mais fundo mergulhamos, maior será a pressão a que estaremos submetidos. Em outras palavras, quanto maior for a profundidade em relação à superfície, maior será a pressão exercida pelo fluido.

A pressão hidrostática relaciona a profundidade, a densidade e a gravidade.

8) A quantidade de fluido ou a substância que o fluido é composto interfere na ação da pressão que ele exerce?

É percebido, em nosso cotidiano, que alguns materiais quando mergulhados em fluidos líquidos, podem afundar ou flutuar sobre o líquido. Isso se deve à ação da pressão que o fluido exerce sobre o material: alguns fluidos exercem sobre diferentes materiais pressões diferentes, dependendo diretamente das substâncias que esses materiais e o fluido são compostos, a essa característica das substâncias damos o nome de densidade de um corpo.

9) O que é densidade de um corpo?

Se colocarmos em uma balança de pratos iguais um recipiente contendo um litro de água e outro contendo um litro de óleo, por experiência, é percebido que os pratos não ficarão equilibrados.

Embora os volumes dos recipientes sejam iguais, a balança indicará diferença entre massa entre eles. Portanto, há mais massa em um litro de água do que em um litro de óleo. Isso significa que a água apresenta uma maior concentração de matéria do que o óleo e nos permite afirmar que, em um recipiente com capacidade volumétrica de um litro, cabe mais massa de água do que de óleo.

O conceito de densidade, exprime a relação entre a massa e o volume. A densidade é a razão entre a massa e o volume.

d = m / V

No SI, a densidade é medida em kg/m³.

Porém, pode ser expresso também em g/cm³ ou g/litro.

10) Com esses conceitos de pressão (p), volume (V), profundidade (h) e densidade (d), é possível expressar as leis que regem a física dos fluidos?

A física dos fluidos ou mais conhecida como hidrostática possui três princípios fundamentais:

a) Teorema de Stiven e ou Equação fundamental da hidrostática: p = h ∙ d ∙ g.

b) Princípio de Pascal: f/a = F/A.

c) Princípio de Arquimedes ou Lei do Empuxo (E): E = d ∙ V ∙ g.

11) O que no diz o Teorema de Stiven?

Além da profundidade, a pressão exercida por um líquido depende de sua densidade e da gravidade no local, uma vez que ela mantém o fluido preso à Terra.

A expressão matemática que possibilita o cálculo da pressão exercida por um fluido líquido resulta da multiplicação da profundidade do local em relação à superfície (h), de sua densidade (d) e do valor da gravidade (g).

p = d ∙ h ∙ g

Denominada equação fundamental da hidrostática, essa expressão mostra que a pressão exercida em um líquido não depende da quantidade do fluido, mas apenas da profundidade. Os engenheiros sabem disso e, quando calculam a espessura da barragem em uma usina hidrelétrica, precisam considerar a profundidade do rio ou da represa.

A equação fundamental da hidrostática mostra também que a pressão exercida por um líquido depende apenas da altura de sua coluna em relação à superfície, conforme a figura abaixo. A forma adquirida pelo líquido não interfere no valor da pressão.

O Teorema de Stiven considera essa equação fundamental como a fórmula da pressão efetiva (p_ef), que corresponde à pressão que uma coluna de líquido exerce num ponto considerado do líquido. Porém para um sistema hidrostático é preciso entender o conceito de pressão absoluta (p_abs), que é a resultante da adição entre pressão atmosférica (p_atm) e pressão efetiva.

Então, finalmente, podemos enunciar o Teorema de Stiven assim: A pressão absoluta num ponto de um líquido homogêneo, incompreensível, de densidade d e numa profundidade h é igual à pressão atmosférica (exercida sobre a superfície desse líquido) mais a pressão efetiva:

p_abs = p_atm + p_ef => p_abs = p_atm + dgh

12) O que nos diz o Princípio de Pascal?

Hoje em dia, é possível utilizar o elevador hidráulico graças a um cientista francês chamado Blaise Pascal (1623-1662), que em 1653 descobriu por meio de experiências que:

Se houver uma variação na pressão exercida sobre um fluido contido em um recipiente, ela é integralmente transmitida a todos os pontos do fluido e às paredes do recipiente que o contém.

A força aplicada na coluna mais estreita de um elevador hidráulico produz uma pressão sobre o fluido, que é transmitida à outra coluna até a sua extremidade.

Além de transmitirem a pressão exercida, esses dispositivos aumentam o módulo da força aplicada graças à ampliação da área de contato na outra extremidade da coluna.

Suponha que a pessoa abra a válvula de ar comprimido ligada ao pistão de área menor (a) e aplicando, assim, uma força de módulo (f). A pressão exercida sobre o fluido poderá ser calculada pela expressão:

p₁ = f / a.

Como essa pressão é transmitida até o outro extremo, cujo pistão tem área maior (A), a força (F), que acionará o sistema mecânico do elevador, também deverá ser maior, de modo que a pressão p₂ seja a mesma.

Isso significa que, se a área da superfície do pistão do elevador for triplicada, a força também será, pois a pressão em ambos os pistões será a mesma.

Essa ampliação de forças é utilizada ainda em prensa, direção e freios hidráulicos. É importante perceber que, em todos esses casos, o pistão menor terá de se deslocar mais que o maior para haver a ampliação da força.

De modo prático, pode ser descrito da seguinte forma:

F₁ / A₁ = F₂ / A₂.

13) O que nos diz o Princípio de Arquimedes?

Observe a Figura abaixo: uma rolha mergulhada num líquido. Note que a rolha se estende por uma certa região do líquido.

Se você levar a rolha até o fundo e depois soltá-la, verá que sobe imediatamente. De fato, para que a rolha suba, é preciso que haja uma força que a empurre para cima. Mas que força é essa? E como ela surge?

Já vimos como a pressão se comporta em relação á força: p = F/A ,e como ela se comporta no interior dos líquidos: a pressão aumenta com a profundidade.

Podemos pensar nela como se fosse formada por vários pedaços: cada um mergulhado numa profundidade diferente. Lembre-se de que a pressão é o resultado da aplicação de uma força sobre uma superfície.

Vamos estudar as forças que atuam nas diferentes partes do corpo. Sabemos que a força é diretamente proporcional à pressão: logo, a força é maior onde a pressão é maior.

Na Figura abaixo as setas indicam as forças que atuam nas diferentes partes dos corpos. Note que o tamanho da seta indica a intensidade da força naquele ponto.

Observe que as forças que atuam na parte de baixo do objeto, isto é, aquelas que tendem a empurrar o objeto para cima, são maiores do que as que tendem a empurrar o objeto para baixo. Somando todas essas forças, vemos que existe uma força resultante força resultante que tem a direção vertical e o sentido para cima. Essa força é o empuxo, e ele que empurra para cima os corpos mergulhados nos líquidos, inclusive a rolha.

Se a pressão não variasse com a profundidade, todas as forças seriam iguais e se anulariam, portanto, a resultante seria zero e não haveria empuxo. Então, um corpo pode boiar graças ao empuxo.

Mas não são todos os corpos que boiam, quando colocados num líquido. Por exemplo um tijolo não boia na água, um pedaço de madeira dependendo do seu tipo pode boiar ou não.

Foi o filósofo e matemático grego Arquimedes, que viveu no século III a.C., quem descobriu, a partir de experiências cuidadosas, como calcular o empuxo, que hoje, modernamente, conhecemos como o Princípio de Arquimedes, e é interpretado da seguinte forma:

Todo corpo mergulhado num líquido recebe um empuxo vertical, para cima, cujo valor é igual ao peso do líquido deslocado pelo corpo.

Então, para calcular o valor do empuxo exercido sobre um corpo, basta calcular o peso do líquido deslocado pelo corpo. Portanto, quanto mais líquido o objeto deslocar, maior será o empuxo.

Podemos obter a expressão matemática para calcular o empuxo sobre um corpo. Dissemos que o empuxo (E) é igual ao peso do líquido deslocado (P_líq): E = P_líq .

O peso é igual ao produto da sua massa, pela aceleração da gravidade.

Portanto: P_líq= m_líq · g ;

assim:

E = m_líq · g.

Como não é usual medir a massa de um líquido, temos uma outra forma mais conveniente de expressar o empuxo, pois sabemos que o líquido é medido pelo seu volume e sabemos de d = m/V e m = d∙V. Desse modo, o empuxo é expresso matematicamente como:

E_líq = d_líq ∙ V_líq ∙ g.

Agora, respondendo a questão porque alguns corpos flutuam e outros afundam, podemos dizer que quando um corpo é mergulhado num líquido, fica sujeito a duas forças: ao seu próprio peso e ao empuxo.

Para saber o que ocorre com o objeto, precisamos estudar a relação entre as forças que agem sobre ele. Podem ocorrer três situações distintas:

P > E; P = E e P < E.

Na tabela abaixo, está um resumo que explica o que ocorre em cada uma das três situações:

14) Uma caixa d’água cúbica ao nível do mar, contem água até a altura de 5 m. Determine a pressão exercida pela água e a pressão absoluta no fundo desse reservatório?

A densidade da água é

d = 1 g/cm³ = 1.000 kg/m³ e g = 10 m/s².

A pressão efetiva será: p_ef = h ∙ d ∙ g.

Então

p_ef = 5 x 1.000 x 10 = 50.000 Pa.

Que corresponde a uma pressão 0,5 atm (a metade da pressão da atmosfera ao nível do mar).

A pressão absoluta será

1 atm + 0,5 atm = 1,5 atm,

que corresponde a 150.000 Pa.

15) Em um elevador hidráulico, um carro de peso 10.000 N está apoiado num êmbolo de 500 cm² de área. Determine o módulo da força que, aplicada a um êmbolo de 25 cm², eleva o carro.

Utilizando o Princípio de Pascal, temos:

F₁ / A₁ = F₂ / A₂

10.000 / 500 = F₂ / 25

F₂ = 500 N.

16) Um corpo de peso igual a 5 N aparenta ter somente 2 N de peso quando completamente mergulhado na água, cuja densidade é 1 g/cm³ (1.000 kg/m³).

Sabendo que g = 10 m/s², determine:

a) o empuxo recebido pelo corpo;

b) o volume do corpo;

c) a densidade do corpo.

a) Nesse caso P > E e o peso aparente P_ap= P – E.

Daí:

2 = 5 – E

E = 5 – 2

E = 3 N

b) Utilizando E_líq = d_liq ∙ V_líq ∙ g e sabendo que como o corpo está totalmente imerso e sabendo que V_líq é o volume do líquido deslocado V_C e portanto o volume do corpo V:

V_líq= V_C = V

Então

3 = 1.000 ∙ V ∙ 10

V = 3 / 10.000

V = 0,0003 m³

V = 300 cm³.

c) Como o peso P = m∙g e o corpo tem peso 5 N, sua massa é

5 = m∙10

m = 5/10

m = 0,5 kg

m = 500 g

Logo a densidade do corpo pode ser dado:

d = m / V

d = 500 / 300

d ≈ 1,7 g/cm³

d = 0,5 / 0,0003

d ≈ 1.700 kg/m³

19) Por que um navio pode boiar? O que podemos dizer sobre a densidade média do navio, quando comparada com a densidade da água do mar?

O corpo do navio é feito de aço, que tem massa específica ou densidade muito mais alta que a da água, deveria, portanto afundar.

O que acontece é que o casco do navio é oco. Logo, apesar da massa específica do ferro continuar mais alta, a densidade do navio diminui, pois a maior parte de seu volume é composta de ar (que tem massa específica muito pequena), para ele boiar a densidade média do navio deve ser menor do que a densidade da água do mar.

Por consequência o empuxo da água do mar suspende o peso do navio.

18) O ar também pode exercer empuxo nos corpos imersos na atmosfera?

O funcionamento de um balão é um exemplo de empuxo. O balão tende a subir devido ao empuxo provocado pelo ar envolta do balão, pois, após o início da queima da bucha, o ar em seu interior fica leve do que o ar fora.

Atividades:

1) Julgue cada afirmativa abaixo como verdadeira (V) ou falsa (F):

a) Exercendo-se sobre o papel a mesma força, um alfinete fura um papel e o lápis não, pois a pressão do alfinete sobre o papel é maior que do lápis. ( )

b) À medida que se desce uma serra a pressão atmosférica vai aumentando. ( )

c) Ao descer para o litoral, a pressão atmosférica aumenta. ( )

d) À medida que uma nave espacial aumenta sua distância em relação a superfície da Terra, a pressão atmosférica diminui. ( )

e) Um balão ganha altitude porque seu peso é praticamente nulo. ( )

f) Um mergulhador a 10 m de profundidade, sofre apenas a pressão exercida pela água do mar. ( )

g) A pressão em um ponto localizado no recipiente contendo líquido é a soma da pressão da coluna acima dele com a pressão na sua superfície. ( )

h) Dois pontos situados no mesmo nível de profundidade em um líquido estão sob a mesma pressão.

i) Na superfície de um líquido a pressão total é nula. ( )

j) A pressão que um líquido exerce sobre o fundo de um recipiente independe de seu formato. ( )

k) Forças de mesma intensidade podem produzir pressões de valores diferentes. ( )

l) O navio pode boiar graças ao empuxo, que é uma força vertical, dirigida para cima, que aparece quando o navio está na água, e que é capaz de sustentar o peso do navio. ( )

2) A pressão atmosférica ao nível do mar, é definida como 1 atm, que corresponde no SI a 10^–5 Pa. O ponto mais alto do Brasil é o Pico da Neblina, com cerca de 3.000 m de altitude. É conhecido que no seu topo a pressão atmosférica internacionalmente é medida em aproximadamente 70.000 Pa. Qual é aproximadamente a pressão no seu topo em atm?

3) Dentro dos pneus existe ar. Como sabemos, o ar é formado por diferentes gases, que exercem pressão sobre as paredes do pneu. Se a pressão lá dentro não estiver correta, o carro ficará instável na pista, por isso é importante que a pressão nos pneus seja sempre verificada, principalmente antes das viagens. Ao levar o automóvel até um posto de gasolina ou oficina que possua o equipamento de calibragem, é comum que o frentista ou o mecânico perguntem se a calibragem vai ser de “28 ou de 30 libras”. Na verdade ele está se referindo a unidade de pressão lbf/pol² (libras-força por polegada ao quadrado) utilizados em equipamentos americanos. Sabe-se que 1 atm equivale a 14,7 lbf/pol².

Qual a pressão em atm de um pneu que deve ser calibrado com 30 lbf/pol² ?

4) Quais das alternativas é correta sobre a densidade?

(A) Depende do formato do material.

(B) Depende da pressão que exerce sobre os corpos.

(D) É a mesma em todas as substâncias.

5) Um litro de álcool etílico possui massa de 800 g. Qual a densidade do álcool etílico em g/cm³ ?

6) Calcule a densidade da solução obtida pela mistura de 1 litro de água com meio litro de outro líquido, sabendo que a densidade da água é 1 g/cm³ e a do outro líquido, de 0,8 g/cm³.

7) Considerando que a superfície de uma piscina ou do mar fica submetida à pressão atmosférica, um mergulhador abaixo dessa superfície está submetido:

(A) à uma pressão atmosférica que o ar exerce sobre o volume de água.

(B) a uma pressão total correspondente à soma da pressão exercida pelo líquido mais a pressão exercida pelo ar.

(D) à pressão que a superfície da piscina ou do mar exerce sobre a água e à atmosfera.

8) Determine, em metros, a que profundidade um mergulhador está, se a pressão total a que está submetido equivale a duas vezes o valor da pressão atmosférica. Considere a densidade da água 1.000 kg/m³ e a pressão atmosférica 100.000 N/m².

9) Despreze a altura da água dentro da caixa, isto é, considere apenas o desnível entre a caixa do edifício e o reservatório. Calcule a pressão com que a água chega à caixa de um edifício, que está a 21 metros do chão, sabendo que a densidade da água é de 1.000 kg/m³.

10) Considere um líquido em um tubo de ensaio. É correto afirmar que:

(A) a pressão exercida por ele em qualquer ponto é a mesma.

(B) a densidade do líquido varia de acordo com a altura em relação à superfície.

(D) a pressão é a mesma em todos os pontos situados a uma mesma altura em relação à superfície.

11) O traje espacial é pressurizado para equilibrar a pressão interna do corpo humano. Sem a pressão externa, a pressão interna do corpo humano não estaria equilibrada e eles “explodiriam”. Dessa forma é necessário:

(A) criar uma pressão externa no interior da roupa espacial, pois a pressão no espaço é muito baixa.

(B) subtrair uma pressão externa no interior da roupa espacial, pois a pressão no espaço é muito alta.

(C) manter o equilíbrio entre o corpo e ausência de pressão atmosfera, mesmo sendo considerada a pressão no espaço a mesma que a do interior da Terra.

(D) manter a temperatura semelhante a da Terra, pois em temperaturas altas, a pressão do corpo humana pode aumentar bruscamente.

12) Quando você toma refrigerante em um copo com canudinho o liquido sobe pelo canudo porque:

(A) a pressão no anterior de sua boca e menor do que a atmosférica.

(B) a pressão atmosférica cresce com a altura ao longo do canudo.

(D) a pressão em um fluido transmite se integralmente a todos os pontos do fluido.

(E) a pressão hidrostática no copo é a mesma em todos os pontos de um plano horizontal.

13) A prensa hidráulica é um dispositivo cujo princípio de funcionamento é explicado pelo:

(A) Princípio de Newton.

(B) Princípio de Galileu.

(D) Princípio de Arquimedes.

14) Considerando o pistão menor de um elevador hidráulico de automóveis, conforme a figura abaixo. Indique a alternativa FALSA, sobre seu acionamento:

(A) O pistão menor é acionado por meio de ar comprimido.

(B) O pistão menor aplica uma força na coluna mais estreita, produzindo uma pressão sobre o fluido, que é transmitida a outra coluna.

(C) O pistão menor transmite a pressão exercida sobre o fluido contido e amplia o módulo da força aplicada sobre o pistão maior, graças ao aumento da área de contato.

(D) O pistão maior reage de forma que a pressão transmitida pelo pistão menor a ele diminua e faz com que a força provocada por um aumento de área suba o elevador.

15) Um elevador hidráulico de um posto de gasolina é acionado por um pequeno êmbolo de área igual a 4 cm². O automóvel a ser elevado tem peso de 20.000 N e está sobre o êmbolo maior de área 1.600 cm². A intensidade mínima da força que deve ser aplicada ao êmbolo menor para conseguir elevar o automóvel é de:

(A) 20 N.

(B) 40 N.

(D) 80 N.

16) Em uma prensa hidráulica que contem um óleo incompreensível e a área do maior êmbolo é 40 vezes a área do menor. Quando um objeto de massa desconhecida é colocada sobre o pistão maior, obtém-se o equilíbrio com uma força de 50 N no pistão menor. O peso desse objeto é:

(A) 40 N.

(B) 100 N.

(D) 2.000 N.

17) Em uma piscina estão três objetos em posições distintas: A está boiando, B está imerso na posição média da profundidade da piscina e C está no fundo.

Nessa situação podemos afirmar que:

(A) a pressão da água em B e C é igual.

(B) a pressão do ar em A é nula.

(D) a pressão da água em B é menor que em C.

18) Em relação à situação do exercício anterior pode-se concluir que:

(A) o peso do objeto é maior que o empuxo em A.

(B) o peso é igual ao empuxo em B.

(D) a força resultante é nula nas três situações.

19) Uma pedra está mergulhada num rio, apoiada sobre o seu leito. Você se abaixa e levanta, mas sem tirá-la da água. Ela parecerá mais leve devido ao empuxo (E): fora da água existe só o peso da pedra (P) e força do braço (F), mas, dentro da água, existe o empuxo, que ajuda a empurrar para cima. Qual a melhor forma abaixo de expressar esse fenômeno:

(A) E > P + F.

(B) E = P = F.

(D) E + P = F.

21) Um tronco está boiando na superfície de um lago. Metade do tronco fica para fora da água, e a outra metade fica imersa. O volume do tronco é 1 m³. Considere a densidade da água do lago como sendo de 1.000 kg/m³ .

a) Calcule o valor do empuxo recebido pelo tronco.

b) Qual o seu peso? E qual a sua massa?

c) Calcule a densidade do material que compõe o tronco.

22) Considere os dados do quadro a seguir.

densidade da agua = 1g/cm³

densidade da agua do mar = 1,03g/cm³

densidade do gelo = 0,9g/cm³

densidade da gasolina = 7,2g/cm³

Pode-se afirmar que:

(A) o gelo flutua na gasolina.

(B) o gelo flutua na água.

(D) o gelo afunda na água do mar.

23) Um rolha de cortiça flutua na água porque:

(A) a cortiça é mais leve que a água.

(B) o empuxo que atua sobre a rolha é maior que o seu o peso.

(D) sua densidade é menor que a da água.

24) As águas do Mar Morto são tão salgadas que não há seres vivos nelas. O clima quente e seco da região produz uma evaporação intensa da água pura e, assim, a quantidade de sal vai aumentando, atingindo cerca de 27% em peso.

Nesse mar, qualquer banhista boia com muita facilidade, pois como a quantidade de sal presente na água é muito alta:

(A) a densidade da água é maior que a do corpo humano.

(B) a densidade da água é menor que a do corpo humano.

(D) a força peso do corpo humano é maior que o empuxo da água.

25) Um artista plástico, querendo chamar atenção para o problema da água, constrói o sistema de vasos comunicantes representado abaixo. Quando a água atingir o nível indicado, podemos afirmar que a pressão no fundo dos vasos é:

(A) maior no vaso B.

(B) igual nos vasos A e C.

(D) maior no vaso C.

(E) maior no vaso D.

26) A massa de um objeto é 80 g e o seu volume 100 cm³. Calculando a sua densidade e sabendo que a densidade da gasolina é 0,70 g/cm³, e a densidade da água 1,00 g/cm³, verifique o que acontece quando o objeto é mergulhado em cada um desses líquidos.

(A) O objeto afundará completamente se mergulhado na gasolina.

(B) O objeto flutuará completamente se mergulhado na gasolina.

(D) O objeto afundará completamente se mergulhado na água.

27) Um dos princípios de maior número de aplicações dentro da hidrostática é o princípio de Arquimedes, pois através dele, podemos explicar, por exemplo, porque um navio flutua ou um submarino pode fundar. Indique, abaixo, a única afirmativa VERDADEIRA:

(A) Um navio, ao passar do mar em que navega para um rio de água doce, cuja densidade é menor do que a ada água salgada, faz com que o volume de líquido por ele deslocado aumente.

(B) Todo corpo total ou parcialmente imerso num líquido recebe um empuxo, debaixo pra cima, igual ao volume de líquido por ele deslocado.

(C) Uma bola colocada, totalmente imersa, em um tanque que contem 20.000 litros de água e posteriormente num jarro que contém apenas 2 litros de água receberá maior empuxo quando submersa no tanque.

(D) Se colocarmos um corpo homogêneo e maciço em um líquido e o corpo flutuar, a densidade do corpo é menor do que a do líquido.

28) (ENEM-2013) Para realizar um experimento com uma garrafa PET cheia d'água, perfurou-se a lateral da garrafa em três posições a diferentes alturas. Com a garrafa tampada, a água não vazou por nenhum dos orifícios, e, com a garrafa destampada, observou-se o escoamento da água conforme ilustrado na figura.

Como a pressão atmosférica interfere no escoamento da água, nas situações com a garrafa tampada e destampada, respectivamente?

(A) Impede a saída de água, por ser maior que a pressão interna; não muda a velocidade de escoamento, que só depende da pressão da coluna de água.

(B) Impede a saída de água, por ser maior que a pressão interna; altera a velocidade de escoamento, que é proporcional à pressão atmosférica na altura do furo.

(C) Impede a entrada de ar, por ser menor que a pressão interna; altera a velocidade de escoamento, que é proporcional à pressão atmosférica na altura do furo.

(D) Impede a saída de água, por ser maior que a pressão interna; regula a velocidade de escoamento, que só depende da pressão atmosférica.

(E) Impede a saída de água, por ser menor que a pressão interna; não muda a velocidade de escoamento, que só depende da pressão da coluna de água.

29) (ENEM-2105) (2ª aplicação) No manual de uma torneira elétrica são fornecidas instruções básicas de instalação para que o produto funcione corretamente:

- Se a torneira for conectada à caixa-d’água domiciliar, a pressão da água na entrada da torneira deve ser no mínimo 18 kPa e no máximo 38 kPa.

- Para pressões da água entre 38 kPa e 75 kPa ou água proveniente diretamente da rede pública, é necessário utilizar o redutor de pressão que acompanha o produto.

- Essa torneira elétrica pode ser instalada em um prédio ou em uma casa.

Considere a massa específica da água 1.000 kg/m³ e a aceleração da gravidade 10 m/s² .

Para que a torneira funcione corretamente, sem o uso do redutor de pressão, quais deverão ser a mínima e a máxima altura entre a torneira e a caixa-d’água?

(A) 1,8 m e 3,8 m

(B) 3,8 m e 7,5 m

(D) 1,8 m e 7,5 m

(E) 18 m e 38 m

Como p = h∙d∙g

p₁ = h₁ ∙ 1.000 x 10 (pressão mínima)

p₂ = h₂ ∙ 1.000 x 10 (pressão máxima)

Pelo manual as pressões são conhecidas, então:

18.000 = h₁ ∙ 1.000 x 10

h₁ = 18.000 / 10.000

h₁ = 1,80 m

38.000 = h₂ ∙ 1.000 x 10

h₂ = 38.000 / 10.000

h₂ = 3,8 m.

30) (ENEM-2012) O manual que acompanha uma ducha higiênica informa que a pressão mínima da água para o seu funcionamento apropriado é de 20 kPa. A figura mostra a instalação hidráulica com a caixa d'água e o cano ao qual deve ser conectada a ducha.

O valor da pressão da água na ducha está associado à altura

(A) h1

(B) h2

(D) h4

(E) h5

Fazendo uso da Lei de Stevin, temos que:

p = h∙d∙g .

Podemos observar que quanto maior a altura, maior a diferença de pressão. Só que essa altura precisa ser medida entre o ponto de saída da água e o ponto onde fica localizado a superfície livre, que nesse caso, seria a caixa d’água. Logo, a maior altura seguindo essa ideia seria a altura h₃.

31) (ENEM-2011) Um tipo de vaso sanitário que vem substituindo as válvulas de descarga está esquematizado na figura. Ao acionar a alavanca, toda a água do tanque é escoada e aumenta o nível no vaso, até cobrir o sifão. De acordo com o Teorema de Stevin, quanto maior a profundidade, maior a pressão. Assim, a água desce levando os rejeitos até o sistema de esgoto. A válvula da caixa de descarga se fecha e ocorre o seu enchimento. Em relação às válvulas de descarga, esse tipo de sistema proporciona maior economia de água.

A característica de funcionamento que garante essa economia é devida:

(A) à altura do sifão de água.

(B) ao volume do tanque de água.

(D) ao diâmetro do distribuidor de água.

(E) à eficiência da válvula de enchimento do tanque.

De acordo com a Lei de Steven citada no enunciado, temos que:

p = h∙d∙g .

É possível ver pela equação que a pressão hidrostática da água é proporcional a altura da coluna de água. Logo, uma das características principais para a economia é o volume de água.

32) (ENEM-2018) Talvez você já tenha bebido suco usando dois canudinhos iguais. Entretanto, pode-se verificar que, se colocar um canudo imerso no suco e outro do lado de fora do líquido, fazendo a sucção simultaneamente em ambos, você terá dificuldade em bebê-lo.

Essa dificuldade ocorre porque o(a):

(A) força necessária para a sucção do ar e do suco simultaneamente dobra de valor.

(B) densidade do ar é menor que a do suco, portanto, o volume de ar aspirado é muito maior que o volume de suco.

(D) peso da coluna de suco é consideravelmente maior que o peso da coluna de ar, o que dificulta a sucção do líquido.

(E) pressão no interior da boca assume praticamente o mesmo valor daquela que atua sobre o suco.

Com o canudo do lado de fora do líquido, não existe diferença de pressão capaz de provocar a subida do líquido, já que a pressão no interior da boca é igual à pressão atmosférica.

33) (ENEM-2019) Dois amigos se encontram em um posto de gasolina para calibrar os pneus de suas bicicletas. Uma das bicicletas é de corrida (bicicleta A) e a outra, de passeio (bicicleta B). Os pneus de ambas as bicicletas têm as mesmas características, exceto que a largura dos pneus de A é menor que a largura dos pneus de B. Ao calibrarem os pneus das bicicletas A e B, respectivamente com pressões de calibração p_A e p_B, os amigos observam que o pneu da bicicleta A deforma, sob mesmos esforços, muito menos que o pneu da bicicleta B. Pode-se considerar que as massas de ar comprimido no pneu da bicicleta A, m_A, e no pneu da bicicleta B, m_B, são diretamente proporcionais aos seus volumes.

Comparando as pressões e massas de ar comprimido nos pneus das bicicletas, temos:

(A) p_A < p_B e m_A < m_B

(B) p_A > p_B e m_A < m_B

(D) p_A < p_B e m_A = m_B

(E) p_A> p_B e m_A > m_B

34) (ENEM-2013) Para oferecer acessibilidade aos portadores de dificuldades de locomoção, é utilizado, em ônibus e automóveis, o elevador hidráulico. Nesse dispositivo é usada uma bomba elétrica, para forçar um fluido a passar de uma tubulação estreita para outra mais larga, e dessa forma acionar um pistão que movimenta a plataforma. Considere um elevador hidráulico cuja área da cabeça do pistão seja cinco vezes maior do que a área da tubulação que sai da bomba. Desprezando o atrito e considerando uma aceleração gravitacional de 10 m/s², deseja-se elevar uma pessoa de 65 kg em uma cadeira de rodas de 15 kg sobre a plataforma de 20 kg.

Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com velocidade constante?

(A) 20 N.

(B) 100 N.

(D) 1.000 N.

(E) 5.000 N.

Pela lei de Pascal: ΔP_A = ΔP_B

f/S_A = F/S_B

f = F ∙ S_A/S_B

Como a cadeira sobe com velocidade constante, temos que existe uma força F que esta em equilíbrio com a força Peso.

F=P_total=1000 N

Se S_B=5S_A

f=1000/5

f=200 N

35) (ENEM-2015) Sabe-se que nas proximidades dos polos do planeta Terra é comum a formação dos icebergs, que são grandes blocos de gelo, flutuando nas águas oceânicas. Estudam mostram que a parte de gelo que fica emersa durante a flutuação corresponde aproximadamente 10% do seu volume total. Um estudante resolveu simular essa situação introduzindo um bloquinho de gelo no interior de um recipiente contendo água, observando a variação de seu nível desde o instante de introdução até o completo derretimento do bloquinho.

Com base nessa simulação, verifica-se que o nível da água no recipiente:

(A) subirá com a introdução do bloquinho de gelo e, após o derretimento total do gelo, esse nível subirá ainda mais.

(B) subirá com a introdução do bloquinho de gelo e, após o derretimento total do gelo, esse nível descerá, voltando ao seu valor inicial.

(C) subirá com a introdução do bloquinho de gelo e, após o derretimento total do gelo, esse nível permanecerá sem alteração.

(D) não sofrerá alteração com a introdução do bloquinho de gelo, porém, após seu derretimento, o nível subirá devido a um aumento em torno de 10% no volume de água.

(E) subirá em torno de 90% do seu valor inicial com a introdução do bloquinho de gelo e, após seu derretimento, o nível descerá apenas 10% do valor inicial.

Pelo Princípio de Arquimedes, o peso do bloco deverá ser é igual ao peso da líquido deslocada. Ao introduzir o bloco de gelo, o volume de água irá subir. No processo de derretimento do gelo não haverá perda de massa e, como a densidade da água é a mesma (para a água do recipiente e para a que antes era gelo), o volume não irá se alterar.

36) A figura abaixo representa dois vasos comunicantes cilíndricos, abertos, contendo dois líquidos não miscíveis A e B, em equilíbrio.

Sejam S_Ae S_B as áreas das superfícies dos líquidos A e B, respectivamente, e d_A e d_B as suas densidades ou massas específicas. Sendo a altura h_A maior que h_B, pode-se concluir que:

(A) h_A∙ S_A = h_B ∙ S_B

(B) h_A ∙ d_A > h_B ∙ d_B