1) Observando o movimento de um antigo brinquedo, conhecido como pião é
percebido que ele se movimento por um bom momento e depois de um instante ele
cai, como é possível explicar esse fenômeno?
O pião não cai por causa do seu movimento de rotação que, por inércia,
tende a resistir a qualquer mudança. Isso quer dizer que ele deve continuar
girando no eixo vertical, e não mudar para o horizontal. Quando o pião começa a
tombar, surge uma força, ligada à velocidade de rotação, que o leva de volta ao
movimento vertical. O pião parece a cabeça de uma pessoa que dorme sentada:
abaixa e logo depois levanta. Depois de um certo tempo, o pião tomba porque o
atrito faz diminuir a velocidade do movimento. Com isso, a força que dá equilíbrio ao pião perde intensidade e
ele cai.
2) Por essa explicação além de existir forças que geram em movimento
existem forças que geram equilíbrio e até mesmo repouso?
Para colocar um corpo em rotação, não é suficiente uma única força. Já
vimos que sempre que um par de forças de mesma intensidade e direção, porém de
sentidos opostos, sobre um corpo em repouso em relação a um referencial, pode
gerar um movimento ou permanecer em repouso, portanto é estabelecida uma
condição fundamental para que na eminência de forças um corpo permaneça em
repouso ou em equilíbrio.
3) Para que um corpo ou ponto
material esteja em equilíbrio que condição precisa ser estabelecida?
Nesse caso, uma única condição deve ser satisfeita: a somatória das forças externas que atuam sobre o corpo deve ser nula. Isso se deve ao fato de que o corpo, no sistema considerado, representa um elemento de dimensões desprezíveis, por isso chamado de ponto material. Desta forma, todas as forças que atuam sobre ele podem ser consideradas concorrentes, isto é, admite-se que elas atuam exatamente no mesmo ponto ou convergem para um mesmo ponto.
4) E no caso de corpos que não podem ser desprezadas as suas dimensões
como é tratado o equilíbrio?
No caso de um corpo extenso, que as dimensões não podem ser
desprezadas, outras considerações devem ser feitas. Quando aplica-se uma força
a um corpo extenso, tem-se que considerar em que ponto do corpo esta força é aplicada. Quando pendura-se o lustre no
teto de uma sala, existe aí um ponto do lustre onde é aplicado a força que o
segura e impede de cair no chão. Nesse momento, a força resultante que atua
sobre ele é nula, porque o módulo da força que a corda, fio ou corrente que segura
o lustre é igual ao módulo do seu peso. E assim ele fica em repouso, ou em equilíbrio estático.
5) No corpo extenso, como é tratado o ponto onde a força é aplicada e
que garante o equilíbrio estático?
Em corpos rígidos, o ponto em que uma força é aplicada pode alterar
radicalmente a situação física. Mas o efeito da força sobre o corpo rígido não
se altera se ela for aplicada em qualquer ponto da reta que contem vetor força. Essa reta é denominada linha de ação da
força. Define-se o momento de uma força
(M0) em relação a um ponto O, também chamado de polo, como sendo:
M0
= F ∙
d,
onde F = intensidade da força;
d = distância do polo à
linha de ação da força.
6) Como é denominado o ponto de equilíbrio dos corpos?
Tente levantar uma vassoura por um cordão amarrado no seu cabo, de tal
forma que ela fique horizontal. Que dificuldade esta simples ação pode
apresentar? Realizando essa atividade sugerida, você vai concluir que existem
apenas um ponto da vassoura no qual o cordão amarrado possibilita que ela, ao
ser suspensa, fique horizontal. Esse ponto é denominado centro de gravidade. Então, podemos definir centro de gravidade
como o ponto de aplicação da resultante das forças de gravidade que atuam em
cada partícula de um sistema, ou o ponto de aplicação da força peso de um
corpo. Geometricamente, é o ponto por onde passa a linha de ação do peso.
7) Como é tratado o equilíbrio de vários corpos aplicando força um
sobre o outro?
Quando temos um corpo aplicando força sobre o outro, é preciso
ressaltar outro conceito, o de centro de
massa, ponto em que se pode admitir que a massa total de um sistema, com um
ou mais corpos em equilíbrio, esteja concentrada. O centro geométrico do objeto
nem sempre coincide com o centro de massa. Existe a possibilidade do centro de
massa estar "fora do corpo”.
Nos campos gravitacionais
uniformes, no qual a gravidade g tem mesmo módulo, mesma direção e mesmo
sentido em todas os pontos da região, como as regiões próximas à Terra, o centro de gravidade coincide com o centro
de massa. Os objetos homogêneos e com formatos geométricos simétricos
possuem centro de massa no “centro”.
8) Duas crianças estão sentadas em extremidades opostas de uma gangorra
de 4,4 m de comprimento. Um dos garotos possui massa de 25 kg, enquanto o outro possui massa de 30 kg. Calcule as distâncias que as crianças devem estar do
ponto de apoio para que a gangorra fique parada na posição horizontal.
Para que um corpo extenso esteja em equilíbrio, são necessárias duas
condições:
a) a resultante das forças externas deve ser nula: ∑F = 0.
b) a somatória dos momentos das forças que atuam no corpo, em relação a
um polo qualquer, deve ser nula: ∑M0
= 0.
O sistema da gangorra pode ser esquematizado da seguinte forma:
(figura do esquema)
Assim, considerando F1 o peso da menina (300N) e d1
a sua distância do ponto de apoio O, e F2 o peso do menino (250N) e
d2 a sua distância do ponto de apoio O, temos:
∑M0 = 0
F1 ∙ d1 – F2
∙ d2 = 0
300
∙ d1 – 250 ∙ d2 = 0
Como d1 + d2 = 4,4 m é o comprimento da gangorra,
temos:
d1 = 4,4 – d2
Combinando as duas equações, temos:
300 ∙ (4,4 – d2) –
250 ∙ d2 = 0
1.320 – 300 ∙ d2 –
250 ∙ d2 = 0
550 ∙ d2 = 1.320
d2 = 2,4 m.
d1 = 4,4 – 2,4
d1 = 2 m.
Logo, para que a gangorra fique
parada na posição horizontal, a menina deverá está a 2 m do centro O e o menino
a 2,4 m do centro O.
9) Onde pode ser utilizado de modo prático a ideia de equilíbrio do
corpos?
Quando abrimos ou fechamos uma
porta com trinco, utilizamos a maçaneta, que é sempre colocada o mais longe
possível das dobradiças. A força aplicada deve ter direção perpendicular ao
plano que contém a porta, para que ela seja aberta com facilidade. Para
utilizar adequadamente um martelo, é necessário segurá-lo o mais distante possível
da outra extremidade. Desses fatos podemos verificar que, quando uma força é
aplicada num corpo rígido, surge uma tendência de rotação em relação a um polo,
essa tendência já vimos que é o momento da força em relação ao polo O, ou como
comumente é chamado de torque.
10) Como é definido e aplicado o torque de uma força?
O torque é definido como grandeza física associada a possíveis rotações
que os corpos possam sofrer. Conhecida também como momento de uma força, o
torque está associado à rotação (giro) que uma força provoca num objeto. Além
do exemplo, do abrir uma porta, e da uma força provoca um giro na maçaneta. O
torque é utilizado no “torque na chave L” que será necessário quando a usamos
para trocar o pneu de um carro, ou em ferramentas e instrumentos como alavanca,
balanços de peso, guindastes, sistema de roldanas e engrenagens, e diversos
outras aplicações que podemos denominar como máquinas mecânicas simples.
11) O que é uma máquina
mecânica simples?
Objetos usados para fazer algo, como alavancas, polias e parafusos são
exemplos de máquinas simples. Uma máquina simples multiplicará uma força, o que
nos ajuda a executar uma função específica.
Uma máquina simples facilita um trabalho, reduzindo a força necessária
para um trabalho.
Exemplos de máquinas simples:
Planos inclinados: uma rampa facilita o movimento de objetos mais
altos.
Cunha: Contém dois planos inclinados, como as laterais de um machado ou
faca.
Parafuso, broca e similares: Estes são planos inclinados que foram
torcidos.
12) Existe distinções entre as máquinas simples?
Existem seis máquinas simples, a saber: alavanca, roda, polia, plano
inclinado, cunha e parafuso.
Destaca-se:
Roda e eixo: pode ser uma roda tradicional com uma pequena haste no
meio.
Alavancas: use uma força para mover uma carga como uma maçaneta da
porta, carrinho de mão ou interruptor de luz.
Polia: uma corda em torno de uma roda que move um objeto para cima e
para baixo.
13) Aplica-se, perpendicularmente, uma força de 4
N para fechar uma porta de 80 cm de largura. Calcule o torque (momento da
força) em relação ao eixo de rotação.
Fórmula do torque (MF):
MF = ± F ⋅
d
d: distância entre o ponto em que a força é aplicada e o eixo de
rotação.
O sinal negativo (−): o giro se dá no sentido horário.
O sinal positivo (+): o giro se dá no sentido anti-horário.
Unidade no SI, utilizada é o N ⋅
m.
Colhendo os dados do problema:
d = 80 cm = 0,8 m
F = 4 N
O giro acontece em sentido horário. O torque será negativo.
Colocando na
equação temos:
MF =
− F ⋅ d
MF =
− 4 ⋅ 0,8
MF =
− 3,2 N ⋅ m
O momento é de −3,2
N ⋅ m
14) O que é importante saber sobre equilíbrio dos corpos?
a) O equilíbrio pode ser: estático ou dinâmico
Equilíbrio estático: o corpo está em repouso (v = 0).
Equilíbrio dinâmico: o corpo está em MRU (v = constante).
O equilíbrio ainda pode ser: instável, estável, semi-estável e indiferente.
b) As condições de equilíbrio
Primeira condição
Das
condições de equilíbrio de um corpo extenso, a primeira é: A força resultante
(Soma de todas as forças) deve ser igual a zero.
ΣF = 0 → FR =
0
F1 +
F2 + F3 + … + Fn = 0
Segunda
condição
Segunda
condição: O momento de forças resultante (a soma de todos os momentos) deve ser
igual a zero.
ΣMF =
0 → MR = 0
MF1 +
MF2 + MF3 + … + MFn = 0
15) Qual deve ser o valor da força do operador (P) aplicada à
alavanca da figura abaixo de forma a mantê-la em equilíbrio?
Todas as vezes que uma alavanca estiver em equilíbrio teremos uma
igualdade entre os momentos das forças de resistência e do operador. O que isso
significa?
O momento é calculado pela multiplicação da força pela distância de seu
ponto de aplicação até o ponto de apoio. Então na condição de equilíbrio
teremos:
Fr ∙
dr = F ∙ d
Nesse exemplo queremos descobrir a força do operador ou força potente,
que é aplicada a 2,40 m do ponto de apoio.
Sabemos da figura que a força de resistência é igual a 20 N e está
aplicada a 1,20 m do ponto de apoio.
Na condição de equilíbrio teremos:
Fr ∙
dr = F ∙ d
Substituindo os valores conhecidos ficamos com:
20 x 1,20 = F ∙ 2,40
24 = F ∙ 2,40 ou F ∙
2,40 = 24
Logo
F = 24 / 2,40
F = 10 N
Ou seja, para que essa alavanca fique parada em equilíbrio a força do
operador ou potente deve ser igual a 10 N.
Atividades:
1) Julgue cada afirmativa
abaixo como verdadeira (V) ou falsa (F):
a) Para sabermos se um ponto
material ou corpo está em equilíbrio, é preciso saber se a primeira lei de
Newton é aplicável a ele. ( )
b) Sempre que a força resultante
sobre um objeto for nula, todas as suas partes estarão em equilíbrio estático.
( )
c) Ponto onde,
hipoteticamente, toda a massa do sistema em equilíbrio está concentrada é sobre
o centro de massa. ( )
d) O centro geométrico de um objeto
nem sempre coincide com o centro de gravidade.
e) Nos campos gravitacionais
uniformes existe uma diferença considerável entre o centro de gravidade e o
centro de massa de um sistema em equilíbrio. ( )
f) Em todo campo gravitacional
uniforme, o centro de gravidade de um corpo está mais próximo da região onde há
maior concentração de massa. ( )
g) Considerando a fórmula do torque MF = ± F ⋅ d, o sinal da operação será positivo quando o giro
for no sentido anti-horário.
h) As maçanetas são colocadas o mais
distante possível do eixo de rotação de uma porta, pois ao aumentar a distância
a força necessária para abrir a porta diminui. ( )
i) Ao utilizar uma chave de
roda para retirar um parafuso na troca de um pneu tem-se uma vantagem mecânica,
pois a força de ação é menor que a força de resistência do parafuso. ( )
j) Não é possível que um corpo
seja submetido a um torque com força resultante nula. ( )
2) Quando um corpo está em equilíbrio estático, qual é a velocidade
dele?
(A) 3
(B) 1
(C) 4
(D) 0
3) A que lei de Newton o
equilíbrio de um ponto material ou corpo está ligado?
(A) Lei da Inércia
(B) Princípio Fundamental da
Dinâmica
(C) Lei de Ação e Reação
(D) Lei da Gravitação
Universal
4) Como se chama a grandeza
física representada por um ponto hipotético onde está concentrada a massa de um
corpo extenso ou de um sistema de partículas?
(A) Força de atrito
(B) Centro de peso
(C) Força peso
(D) Centro de massa
5) Como é chamada a grandeza
física associada a possíveis rotações que os corpos possam sofrer?
(A) Aceleração
(B) Torque
(C) Massa
(D) Trabalho
6) Qual destes NÃO é um tipo
de máquina mecânica simples?
(A) Alavanca
(B) Alicate
(C) Mesa
(D) Gangorra
7) Um
corpo rígido esta em equilíbrio sob a ação de um sistema de três forças. Qual
das alternativas abaixo descreve melhor a situação?
(A) A
resultante das forças deve ser nula.
(B) O
momento das forças deve ser nulo.
(C) A
resultante das forças deve ser diferente de zero.
(D) A soma
dos momentos e a resultante das forças devem ser nulas.
8) Ao se fechar uma porta, aplica-se uma força na maçaneta para ela rotacionar em torno de um eixo fixo onde estão as dobradiças. Com relação ao movimento dessa porta, indique a única alternativa CORRETA:
(A) Quanto maior a distância
perpendicular entre a maçaneta e as dobradiças, menos efetivo é o torque da
força.
(B) A unidade do torque da
força no SI é o N∙m, podendo também ser medida em Joule (J).
(C) O torque da força depende
da distância perpendicular entre a maçaneta e as dobradiças.
(D) Qualquer que seja a
direção da força, o seu torque será não nulo, consequentemente, a porta
rotacionará sempre.
9) Um portão está fixo em um
muro por duas dobradiças A e B, conforme mostra a figura, sendo P o peso do portão.
Caso um garoto se dependure no
portão pela extremidade livre, e supondo que as reações máximas suportadas
pelas dobradiças sejam iguais, podemos dizer que:
(A) é mais provável que a
dobradiça A arrebente primeiro que a B.
(B) é mais provável que a
dobradiça B arrebente primeiro que a A.
(C) seguramente as dobradiças A e B arrebentarão simultaneamente.
(D) nenhuma delas sofrerá qualquer esforço.
(E) o portão quebraria ao meio, ou nada sofreria.
10) Uma calça molhada de 500 g
está pendurada em um varal. Considerando a gravidade no local igual a 10 m/s2
é correto dizer que:
(A) o peso da calça é de 500
N.
(B) a força que o varal faz
sobre a calça deve ser de 50 N para que ela permaneça em equilíbrio estático.
(C) para que haja equilíbrio
estático, a força resultante aplicada sobre a calça deve ser 0.
(D) na força resultante sobre
a calça igual a 0, é possível o equilíbrio dinâmico.
11) Um homem faz uma força
perpendicular de 5 N para fechar uma porta de 90 cm de largura. Qual é o torque
(momento da força) em relação ao eixo de rotação?
12) Uma criança pesando 400 N
está sentada numa extremidade de uma gangorra de 3 m de comprimento e apoiada a
1,4 m da criança. Se outra criança estiver apoiada na outra extremidade,
equilibrando a gangorra, qual o seu peso? Qual a força total no apoio?
13) Como equilibrar uma
gangorra de playground com uma pessoa de massa 60kg em um lado e uma criança de
30 kg no outro?
(A) A pessoa mais leve deve
ficar duas vezes mais distante do ponto de apoio que a pessoa mais pesada.
14) A barra da figura é um
corpo rígido de peso desprezível, apoiada no ponto P. Qual o módulo da força
que mantém a barra em equilíbrio mecânico na posição horizontal?
(A) 10 N
(B) 20 N
(C) 30 N
(D) 40 N
15) A
barra AB é uniforme, pesa 50 N e tem 10 m de comprimento. O bloco pesa 30 N e
dista 8 m de A. A distância entre os pontos de apoio da barra é AC = 7 m.
Nessas
condições, a reação no ponto A vale:
(A) 0,4 m
à esquerda de B.
(B) 0,4 m
à direita de B.
(C) 0,1 m
à esquerda de B.
(D) 0,1 m
à direita de B.
16) Um homem de peso 600 N
caminha numa tábua de madeira simplesmente apoiada em uma extremidade A e
articulada em C, distante 4 m de A. O peso da tábua é 900 N e seu comprimento é
de 6 m. Determina a máxima distância x, indicada na figura, que o homem pode
caminhar sobre a tábua para que ela fique em equilíbrio.
17) Um homem de massa 80kg
quer levantar um objeto usando uma alavanca rígida e leve. Os braços da alavanca
têm 1 m e 3 m.
a) Qual a maior massa que o
homem consegue levantar usando a alavanca e seu próprio peso?
b) Nesse caso, qual a força exercida
sobre a alavanca no ponto de apoio?
18) Uma pessoa A, tentando
fechar uma porta, aplica a uma maçaneta uma força F = 40N, tentando fazer-se
girar no sentido horário.
a) Sabendo que a maçaneta
dista 90 cm das dobradiças, determine o torque que a pessoa aplica a porta ?
b) Uma pessoa B consegue
impedir que a porta seja fechada, aplicando uma força F´. Qual o torque que B
aplicou a porta?
c) Qual o valor de F´ se ela
foi aplicada a 20 cm das dobradiças ?
19) Na figura abaixo,
suponha que o menino esteja empurrando a porta com uma força Fm = 5
N, atuando a uma distância 2 m das dobradiças (eixo de rotação), e que o homem
exerça uma força Fh = 80 N, a uma distância de 10 cm do
eixo de rotação.
Nestas condições, pode-se
afirmar que:
(A) a porta estaria girando no
sentido de ser fechada.
(B) a porta estaria girando no
sentido de ser aberta.
(C) a porta não gira em nenhum
sentido.
(D) o valor do momento
aplicado à porta pelo homem é maior que o valor do momento aplicado pelo
menino.
(E) a porta estaria girando no
sentido de ser fechada, pois a massa do homem é maior que a massa do
menino.
20) Para girar a porca que
prende a roda de um veículo é necessário um torque de 120 N∙m.
Supondo que a força máxima que uma pessoa consegue exercer é de 500 N, qual o
comprimento mínimo da chave de roda para que ela consiga realizar a tarefa ?
21) É comum encontrarmos em
manuais de motos o valor do torque máximo que pode ser aplicado em uma porca.
Do manual de uma moto, por exemplo, consta a seguinte informação: "torque máximo para aperto da porca do
eixo dianteiro 70 N∙m". Se um mecânico usa uma chave de boca que permite um braço máximo de
0,14 m. Qual é a maior força que ele pode aplicar na ferramenta sem danificar a
porca (para o braço máximo)?
22) Determine
o módulo dos torques para cada uma das forças aplicadas na ferramenta em
relação ao eixo que passa pelo ponto O. Dados: F1 = F2 = F3
= 10N.
23) (ENEM-2015) Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.
Nessa situação, qual foi a massa da barra obtida pelos alunos?
(A) 3 kg
(B) 5 kg
(C) 6 kg
(D) 15 kg
24) O bíceps é um dos músculos envolvidos no processo de dobrar nossos braços. Esse músculo funciona num sistema de alavanca como é mostrado na figura ao lado. O simples ato de equilibrarmos um objeto na palma da mão, estando o braço em posição vertical e o antebraço em posição horizontal, é o resultado de um equilíbrio das seguintes forças: o peso P do objeto, a força F que o bíceps exerce sobre um dos ossos do antebraço e a força C que o osso do braço exerce sobre o cotovelo. A distância do cotovelo até a palma da mão chamamos de a e a distância do cotovelo ao ponto em que o bíceps está ligado a um dos ossos do antebraço de d.
Com base nos conceitos de
alavanca interpotente analise o texto acima e identifique a alternativa
correta.
(A) A força potente (F) é
sempre menor que a força resistente (P).
(B) A
força potente (F) é sempre maior que a força resistente (P).
(C) A força potente (F) e a
força resistente são iguais (P).
(D) A força potente (F) e a
força resistente (P) podem ser iguais ou diferentes.
(E) Não podemos fazer
quaisquer afirmações a respeito das forças potente e resistente.
25) Um estudante de engenharia desenvolveu o projeto de um braço mecânico capaz de abrir e fechar portas a partir de um comando de voz. O equipamento deveria ser instalado atrás da porta e, a partir de um determinado comando, teria capacidade de rotacionar o sistema. Na montagem do sistema, o braço mecânico foi instalado de forma que a posição onde exercia a força capaz de rotacionar a porta correspondia à metade da largura desta. O projeto não foi avaliado com a nota máxima porque:
(A) não há relevância no desenvolvimento de um braço mecânico com a finalidade de abrir portas.
(B) a rotação da porta seria impossível se o braço mecânico fosse instalado na posição planejada.
(C) o braço deveria ser instalado o mais próximo possível das dobradiças para que a rotação do sistema fosse executada com um menor esforço.
(D) o braço deveria ser instalado o mais distante possível das dobradiças para que a rotação do sistema fosse executada com um menor esforço.
(E) a posição escolhida para a instalação do braço mecânico corresponde à posição onde o esforço para rotação da porta é máximo.
26) Um casal namora em um
balanço, cujo assento de madeira está preso ao teto por duas cordas verticais.
A moça tem massa 50 kg e o rapaz 70 kg. A massa do balanço é desprezível.
Na situação da figura, o balanço está em equilíbrio estático e os centros de
gravidade da moça e do rapaz distam 0,30 m e 0,58 m da corda mais próxima,
respectivamente. Sendo 1,28 m a distância que separa as duas cordas e g = 10
N/kg, qual é a tração em cada corda?
A lógica pra resolução desse problema é a
seguinte: Temos forças e torques atuando no sistema. Porém, está em equilíbrio
estático. Isso significa que a soma das forças e a soma dos torques é igual a
zero, o que nos resulta em duas equações (soma das forças; soma dos torques) e em
duas incógnitas (tração em cada uma das cordas). Então vamos lá, primeiramente,
desenhando todas as forças do sistema.
Observe na imagem acima que T1 e T2 são as forças de
tração das cordas, P1 é a força peso da moça e P2 a força peso do rapaz. O
ponto médio que desenhei, PM, é o ponto que divide exatamente o balanço ao
meio, ou seja, onde a distância da corda até o PM é igual a metade da distância
entre as cordas: 1,28/2 = 0,64 m. Esse será nosso ponto de referência para o
cálculo dos torques.
Primeiramente, vamos calcular o somatório
das forças, que deve ser igual a 0. Aqui precisamos considerar que as forças
para cima são positivas e as forças para baixo são negativas.
∑F = 0
T1 + T2 + (-P1) + (-P2) = 0
P1 e P2 são os pesos da moça e do rapaz,
calculados por: P = m . g, onde m é a massa e g é a aceleração da gravidade.
Portanto:
P1 = 50 kg . 10 N/kg = 500 N
P2 = 70 kg. 10 N/kg = 700 N
Sendo assim:
T1 + T2 – 500 – 700 = 0
T1 + T2 = 1200 N
Essa é a nossa primeira equação.
Agora vamos calcular a equação dos torques,
cujo somatório deve ser igual a 0. Vamos chamar o torque pela letra N. Sabemos
que o torque é dado por N = F.d, onde F é a força e d é a distância.
∑N = 0
∑(F.d) = 0
O nosso ponto de referência para determinar
as distâncias é o centro de gravidade (PM) do balanço, que é o objeto sobre o
qual as forças estão atuando. Assim, a distância de T1 ao PM é metade da
distância entre as cordas, que é 0,64 m. O mesmo é de T2 até PM. Já a distância
de P1 ao PM é dada por 0,64 – 0,30 = 0,34 m. De P2 ao PM a distância é 0,64 –
0,58 = 0,06 m.
Consideraremos que as forças à direita do
PM resultarão em um torque positivo e as forças à esquerda do PM
resultarão em um torque negativo, bem como as forças para baixo são
negativas e as forças para cima são positivas.
(–T1 . 0,64) + (T2 . 0,64) + (–(–P1 . 0,
34)) + (–P2 . 0,06) = 0
0,64 . (T2 – T1) + (500 . 0,34) – (700 .
0,06) = 0
0,64 . (T2 – T1) + 170 – 42 = 0
0,64 . (T2 – T1) = -128
T2 – T1 = -200 N
Assim temos a segunda
equação, formando um sisteminha de duas equações com as incógnitas T1 e
T2.
Isolando T2 na segunda equação:
T2 = T1 – 200
Substituindo na primeira equação
T1 + T1 – 200 = 1200
2T1 = 1400
T1 = 700 N
Voltando para a segunda equação
T2 = 700 – 200
T2 = 500 N
Sendo assim, as forças de tração das cordas
são 700 N para a corda mais próxima da moça e 500 N para a corda mais próxima
do rapaz.
27) (ENEM-2012) O mecanismo que permite articular uma porta (de um móvel ou de acesso) é a dobradiça. Normalmente, são necessárias duas ou mais dobradiças para que a porta seja fixada no móvel ou no portal, permanecendo em equilíbrio e podendo ser articulada com facilidade.
No plano, o diagrama vetorial das forças que as dobradiças exercem na
porta está representado em:
Opção (D)
A porta tende a girar para o
sentido horário, ao fazer isso, a porta irá prover uma tração, horizontal, na
dobradiça superior e comprimir a inferior. Pelas leis de Newton, essas
dobradiças reagem na porta com uma força Fh1 para a
superior e Fh2 para a inferior. Além disso, temos também
componentes de forças verticais que chamaremos de Fv1 e
Fv2, respectivamente, que juntas anulam a força peso
da porta.
Logo, temos que:
FR1=Fh1+Fv2
FR2=Fh2+Fv2
Pesquisa Google:
1) O que é equilíbrio instável
?
2) O que é equilíbrio estável
?
3) O que é equilíbrio
semi-estável ?
4) O que é equilíbrio indiferente ?
Cálculo do Centro de Massa de um corpo ou Baricentro
Representamos o centro de massa por um ponto C, composto por coordenadas.
No plano bidimensional, o ponto C será o par
ordenado (xCM, yCM).
Calcula-se as coordenadas pela média ponderada dos
pontos:
xCM = (m1x1 +
m2x2 + m3x3) / (m1 +
m2 + m3)
yCM = (m1y1 +
m2y2 + m3y3) / (m1 +
m2 + m3)
Gráfico
O gráfico representa um sistema de partículas.
Calcule as coordenadas do centro de massa.
Colhendo as coordenadas de cada ponto temos:
x1 = 0, x2 = 2 cm e
x3 = 3 cm
y1 = 3 cm, y2 = 1
cm e y3 = 4 cm
Cálculo x
Cálculo da coordenada x do centro de massa:
xCM = (4 ⋅ 0 + 5 ⋅ 2 + 2 ⋅ 3) / (4 + 5 + 3)
xCM = (0 + 10 + 6) / 12
xCM = 16/12
Simplificando, temos:
xCM = 4/3
Cálculo y
Cálculo da coordenada y do centro de massa:
yCM = (4 ⋅ 3 + 5 ⋅ 1 + 2 ⋅ 4) / (4 + 5 + 3)
yCM = (12 + 5 + 8) / 12
yCM = 25/12
Aprofunde-se:
Máquinas simples
O ser humano, ao longo de sua história, sempre procurou melhorar suas condições de trabalho, principalmente no que se refere à redução de seu esforço físico. Assim, buscou meios alternativos que lhe permitisse realizar as tarefas de modo mais fácil e com o menor gasto possível de tempo e de sua força muscular.
Os primeiros instrumentos
utilizados foram a alavanca, a roda e o plano inclinado que, por sua
simplicidade, ficaram conhecidos como máquinas simples.
Alavanca
Alavancas são máquinas
simples.
Uma alavanca é composta por 3
partes: ponto de apoio, força resistente, força potente.
Existem três tipos de
alavanca.
Interfixa: O ponto fixo está
entre a força potente e a força resistente. Ex: tesoura.
Interpotente: A força potente
está entre a força resistente e o ponto fixo. Ex: pinça.
Inter-resistente: A força
resistente está entre a força potente e o ponto fixo. Ex: carrinho de mão.
A utilização de máquinas
simples oferece grandes vantagens na realização de trabalhos, pois permite que
você use menos força para realizar tarefas como, por exemplo, para deslocar ou
levantar grandes pesos.
Para entendermos sua
importância nos dias de hoje, basta imaginar o que seria de nós sem as
máquinas.
A alavanca é basicamente uma
barra que pode girar em torno de um ponto de apoio. Quando você usa um pedaço
de pau para deslocar uma pedra, um quebra-nozes, um cortador de pinhão ou uma
pinça de confeitaria para pegar um pão ou um doce, você está usando uma alavanca.
Criança na gangorra, exemplo de alavanca. Crédito: imagem comunitária.
Disponível em https://www.vecteezy.com/vector-art/73990-girl-on-seesaw Acesso em 17/09/18.
Classificação das alavancas
Dependendo das posições
relativas das posições ocupadas pela força do operador ou potente (F ou P),
ponto de apoio (PA ou O) e força de resistência (Fr ou R), as alavancas
classificam-se em:
Alavancas do primeiro gênero
ou interfixas - Ordem: ROP, ou seja, com o ponto de apoio localizado entre a
força de resistência e a força potente. Exemplos: tesoura, martelo quando usado
para retirar pregos e escavadeira.
Alavancas do segundo gênero ou
inter-resistentes - Ordem: ORP, ou seja, possuem o ponto de apoio em um dos
extremos da barra. Localizado próximo ao ponto de apoio está a força de
resistência e mais distante está a força potente. Exemplos: quebra-nozes,
carrinho de mão, abridor de garrafas e o movimento do ser humano de ficar
apoiado nas pontas dos pés.
Alavancas do terceiro gênero
ou interpotentes - Ordem: OPR, ou seja, possuem o ponto de apoio em um dos
extremos da barra. Localizado próximo ao ponto de apoio está a força potente, e
mais distante está a força de resistência. Exemplos: pinça, vara de pescar,
segurar uma bola na mão com o braço mantido a 90°.
Roda
Outra máquina, a princípio, simples bem utilizada, e posteriormente bem desenvolvida é a roda.
A roda. Crédito:
Jörgens.mi, CC BY-SA 3,0. Disponível em https://commons.wikimedia.org/wiki/File:Vanvooren_(Volante)_jm20668.jpg.
Acesso em 17/09/18.
A roda certamente foi uma das descobertas mais importantes da humanidade, apesar de ninguém saber ao certo sua origem. Na pré-história, os homens usavam troncos de árvores e discos de pedra para exercerem as funções das rodas, facilitando o deslocamento de grandes cargas por longas distâncias. Provavelmente, a roda surgiu sob a forma de rolete.
A roda usada antigamente no transporte de canhões. Crédito: autor desconhecido, Domínio público. Disponível em https://commons.wikimedia.org/wiki/File:18-pounder_field_gun_with_sand_wheels_Suez_Canal_1916_IWM_Q15840.jpg. Acesso em 17/09/18.
Além da roda várias ferramentas foram inventadas ao longo da história da humanidade, por exemplo, arado, arco e flecha, catapultas.
Arado de madeira puxado a cavalo. Crédito: U.S. National Archives and Records Administration, Domínio público. Disponível em https://commons.wikimedia.org/wiki/File:Horse_pulling_plow_-_NARA_-_285314.jpg. Acesso em 17/09/18.
Hoje, as máquinas são muito mais complexas e geram riquezas pela produção de bens, além de facilitarem nossas vidas, economizando nosso tempo e força na realização de tarefas.
Catapulta. Crédito:
Luís Sequeira, CC-BY-2,0. Disponível em https://commons.wikimedia.org/wiki/File:Penedono,_catapulta_(5987340890).jpg.
Acesso em 17/09/18.
Engrenagens
Um multiplicador de força nos
permite liberar uma grande força ao aplicar uma pequena força.
As engrenagens são um exemplo
de máquina simples que multiplica forças.
Uma engrenagem é formada por
duas ou mais rodas dentadas que se interligam.
Usamos engrenagens em uma
bicicleta. Se você pedalar uma montanha, você quer uma marcha baixa, que exige
menos esforço na primeira marcha.
Faca
Uma faca tem
dois planos inclinados para que ela deslize para o que você deseja cortar. É uma
máquina porque multiplica a força aplicada.
Um multiplicador de força nos permite liberar
uma grande força ao aplicar uma pequena força.
Recomendamos que você use este tutorial na seguinte ordem:
Primeiro: Analise o que está acontecendo em cada um dos vídeos silenciosos de exploração das máquinas simples;
Segundo: Identifique as partes de cada
máquina simples e observe o que está acontecendo com cada uma delas e entre
elas;
O que é preciso fazer para
reequilibrar o nível quando o ponto de apoio é deslocado para o lado direito?
O que acontece com a distância
entre a extremidade esquerda e o ponto de apoio quando esse último é deslocado
para a direita?
Quando o ponto de apoio é
deslocado para a direita, qual extremidade adquire uma vantagem mecânica? E
qual extremidade fica em desvantagem mecânica?
Polias
Atenção: alguns dos vídeos abaixo não possuem som.
Eles são mudos para que você faça suas próprias
observações e anotações para responder as perguntas sobre os mesmos.
A utilização de uma polia conforme o arranjo mostrado
no vídeo traz alguma vantagem mecânica?
Se não traz nenhuma vantagem por que você usaria esse
arranjo de polia?
O vídeo abaixo também não possui som.
Por que tem duas polias fixas no topo da estrutura?
Qual a distância percorrida pela gôndola da direita
comparada com a da esquerda?
Qual das duas gôndolas tem vantagem mecânica, ou seja,
influencia mais no deslocamento?
O vídeo abaixo não tem som.
Por que são usadas duas polias no topo da gôndola da
esquerda?
Qual a distância deslocada pela gôndola da esquerda
comparada com a da direita?
Qual gôndola tem vantagem mecânica?
Agora vamos ver um vídeo com um sistema motorizado de
polias usado para erguer uma carga bem pesada.
O que você faria para arrumar a inclinação da carga na primeira parte do vídeo?
Qual é a vantagem mecânica do sistema mostrado no final do vídeo? (Dica: preste atenção na polia móvel no centro da estrutura)
Qual gôndola tem a maior
vantagem mecânica quando o um à esquerda for movido mais perto para
o eixo da "roda"? Por que?
Onde está o lado da borda
da "roda'' para a gôndola na esquerda depois que ela for movida?
Por que as peças retas de LEGO anexadas ao ponto de engrenagem em ângulos diferentes quando a gôndola da esquerda é movida?




































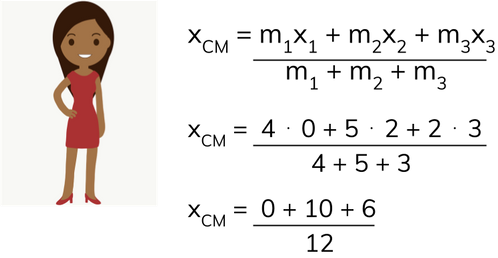













Nenhum comentário:
Postar um comentário